leetcode-5.最长回文子串-manacher
|Word count:779|Reading time:3min|Post View:
Question:给你一个字符串 s,找到 s 中最长的回文子串。
leetcode-5
该题使用马拉车算法解时间复杂度和空间复杂度均为O(n)
manacher思想介绍:
一、(center) C 为回文串对称中心坐标
二、(radius) R[C] 以C为对称中心的回文串半径
三、(iterator) I 对称中心在R[C]范围内,且I>C的回文串对称中心坐标
四、(Point) P以C为中心,回文串结束的下标
下面假设有一个字符串,i‘为i的对称点
此时R[i]有两种情况,R[i]≤P或R[i]>P
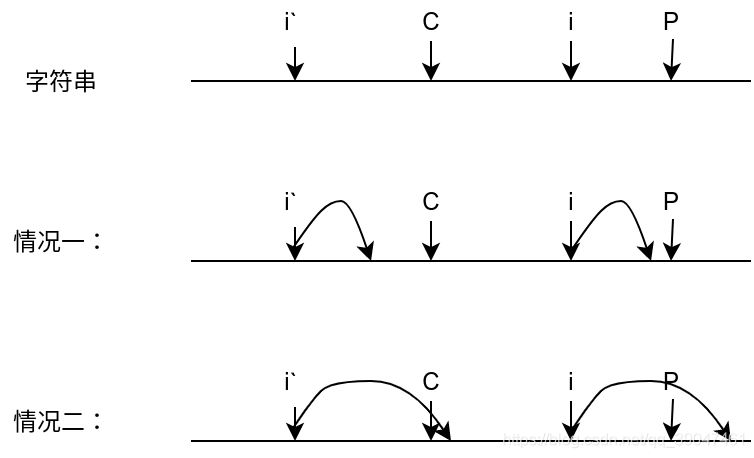
情况一: 由于i‘是已经遍历过的位置,所以存在 R[i‘]>0&&R[i‘]==R[i] ,但此时p点之后的情况是未知的,故将R[i]赋值为min(R[i‘],P−i),为的是保证i+R[i]≤P
情况二: 由于i+R[i]>P, 故将C点状态转移到i点。
分析完马拉车的两种情况之后可以得出代码套路:
- 将字符串进行处理,方便统计
- 对字符串进行遍历,利用对称关系和辅助数组,遍历一遍即可得到最长回文子串的对称中心所在。
- 然后将答案处理至答案数组。
STEP1: 由于字符串长度分奇偶,首先将字符串处理,在字符串中加入一个没有的字符, 如 ==‘#’==,处理后的字符串性质无改变,只是将奇偶情况合并为一种情况,得到辅助字符串。如 :
原字符串回文串为==偶数== abbad -> #a#b#b#a#d# 此时原字符串的对称中心由bb之间转换为#,
原字符串回味串为==奇数== abad -> #a#b#a#d# 此时对称中心还是b
STEP2: 根据两种情况对字符串进行遍历得到辅助数组R
STEP3: 遍历辅助字符串,根据辅助数组求得最长的字符串;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public:
string getnewstring(string str) {
string news = "#";
for (int i = 0; i < str.size(); i++) {
news += str[i];
news += '#';
}
return news;
}
string longestPalindrome(string s) {
string ns = getnewstring(s);
int *r = new int[ns.size()], c;
r[0] = 1, c= 0;
for (int i = 0; i < ns.size(); i++) {
if (i >= c + r[c]) {
r[i] = 1;
} else {
r[i] = min(r[2 * c - i], c + r[c] - i);
}
while (i - r[i] >= 0 && ns[i - r[i]] == ns[i + r[i]]) {
r[i]++;
}
if (c + r[c] < i + r[i]) c = i;
}
int ans = 0;
string S = "";
for (int i = 0; i < ns.size(); i++) {
if (r[i] <= ans) continue;
ans = r[i];
S = "";
for (int j = i - r[i] + 1; j < i + r[i]; j++) {
if (ns[j] == '#') continue;
S += ns[j];
}
}
return S;
}
};
|



